👀 Gaze-Based Learning from Demonstration in Surgical Robotics

Special thanks to my teammates: Jaden Ingleton, Sayem Zaman, and Trent Suzuki :)

Introduction

Project Overview

In the fourth year of my engineering physics degree, we had to take the project development + management course ENPH 459 Engineering Physics Project II, where we tried to complete an open-ended engineering project sponsored by companies in the industry, professors or research labs in 8 months. Aside from the engineering aspect of the project, we were expected to manage the project from start to finish, i.e. define scopes and limitations of the project, propose our solutions to our sponsors, perform risk analysis and weekly reportings, etc. We also had to present our project and ideas professionally and treat it like an investor/stakeholder presentation. At the end of the project, we participated in the project fair, showcased our results and wrote a formal final report.

Problem Statement

In the field of robotic assisted surgery, the da Vinci robot, designed and manufactured by Intuitive Surgical has been the most developed and researched system in the past 20 years. Currently, while using the da Vinci system, surgeons control the surgical camera and the robot arms using two hand-held controllers. To switch between control modes, the surgeon has to relinquish control of the arms, which interrupts the flow of the operation. The main goal of this research is to automate the motion of the endoscopic camera arm using a probabilistic model based on eye gaze data and robot kinematic data. The model will take in the expert surgeons’ eye gaze data and robot kinematic data of the surgical scene to learn how to automate the camera movement.

For a more in depth introduction and problem statement, please check out our final report.

Method

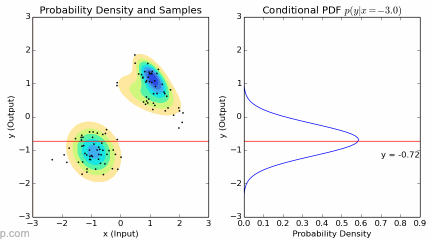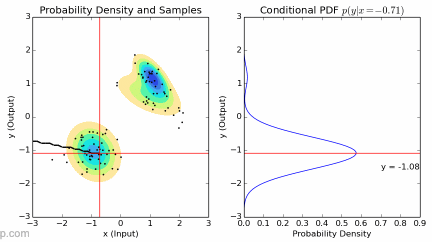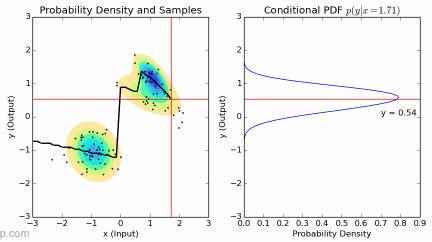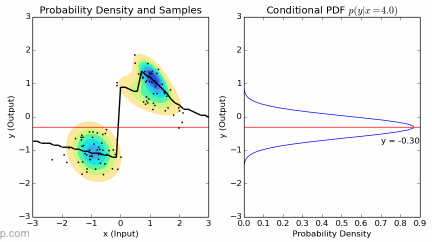
To solve this problem, the method we came up with is learning from demonstration (LfD). Basically, we proposed to let the surgeons “demonstrate” how the camera arm should move by just letting them perform surgery and control the camera arm using the foot pedal. Then, we will filter out the data when the camera arm is not moving and gather the surgeon eye gaze, robot arms’ position and orientation from the remaining set of data. Finally, we will train the model on the processed data set. After optimizing the training parameters and appropriate data cleaning, we will eventually end up with a model that can predict the camera arm movement in real time based on previous “demonstrations”.

We chose to train a type of machine learning model called Gaussian Mixture Model (GMM) and predict the outcome using Gaussian Mixture Regression (GMR). Since this method is a bit too technical to be included here, I have embedded the final report below which has the full explanation for GMM/GMR, including more in depth explanations and procedures.

It is worth mentioning that we initially chose Matlab as our main language to implement the GMM training and GMR prediction, but it is too inefficient and difficult to optimize. It takes around 20 minutes to complete a model that only takes in 9 dimensional data with up to 20 Gaussians. We migrated our codebase to Python and incorporated this API into our implementation. This greatly sped up the computing process and helped us push forward to the deployment phase.

class GMR():

    def gaussianMixtureRegression(self, input, means, covar, inputCols=list(range(6)), outputCols=list(range(6, 9))):
        '''Adapted from MATLAB function with the same name'''
        self.miuInput  = means[:, inputCols]
        self.miuOutput = means[:, outputCols]

        # Covariances (sigma)
        self.covInput = covar[inputCols, :, :]
        self.covInput = self.covInput[:, inputCols, :]

        self.covOutput = covar[outputCols, :, :]
        self.covOutput = self.covOutput[:, outputCols, :]
        
        self.covInOut = covar[inputCols, :, :]
        self.covInOut = self.covInOut[:, outputCols, :]
        
        self.covOutIn = covar[outputCols, :, :]
        self.covOutIn = self.covOutIn[:, inputCols, :]

        ## * * * Computing the conditional expectation and variance given input * * *                           
        self.numPts     = input.shape[0]  # Number of query points
        self.numGauss   = means.shape[0]  # Number of gaussians
        self.numOutputs = len(outputCols)  # Number of output dimensions

        self.condY = np.zeros((self.numPts, self.numOutputs, self.numGauss))
        # Conditional expectation ŷi for every query points
        for i in range(self.numGauss):
            # Computing difference between each input point and input mean (miu_xj)
            diff = (input - np.ones((self.numPts, 1)) * self.miuInput[i, :]).T
            # Computing conditional expectation ŷ for j-th gaussian
            self.condY[:, :, i] = (np.ones((self.numPts, 1)) * self.miuOutput[i, :]) + \
                ((self.covOutIn[:, :, i] @ np.linalg.inv(self.covInput[:, :, i])) @ diff).T
            # print(self.condY[:, :, i])

        self.condSigma = np.zeros((self.numOutputs, self.numOutputs, self.numGauss))
        # Conditional covariance sigma_j (estimated)
        for i in range(self.numGauss):
            self.condSigma[:, :, i] = self.covOutput[:, :, i] - \
                (self.covOutIn[:, :, i] @ np.linalg.inv(self.covInput[:, :, i])) @ self.covInOut[:, :, i]
            # print(self.condSigma[:, :, i])

        ## * * * * Computing responsibilities of each Gaussian given input * * * *
        # Conditional probability of x given j-th gaussian
        self.pxi = np.zeros((self.numGauss, self.numPts))
        for i in range(self.numGauss):
            self.pxi[i, :] = self.gaussianPDF(input, self.miuInput[i, :], self.covInput[:, :, i])

        # Responsibilities for each gaussian
        self.hi = np.zeros((self.numGauss, self.numPts))
        for i in range(self.numPts):
            self.hi[:, i] = self.pxi[:, i] / sum(self.pxi[:, i])

        self.computeExpectationMixture()
        self.computeSigmaMixture()


    def computeExpectationMixture(self):
        ## * * * Computing conditional expectation and variance of the mixture * * *
        # Conditional expectation ŷ of the resulting mixture given input
        self.condYmixt = np.zeros((self.numPts, self.numOutputs, self.numGauss))
        for i in range(self.numGauss):
            self.condYmixt[:, :, i] = self.condYmixt[:, :, i] + \
                ((np.expand_dims(self.hi[i, :], axis=1) @ np.ones((1, self.numOutputs))) * self.condY[:, :, i])
        #     if i == 0:
        #         print(self.condYmixt[:, :, i])
        # print(len(self.condYmixt))
        self.output = np.sum(self.condYmixt, axis=2)


    def computeSigmaMixture(self):
        # Conditional variance sigma of the resulting mixture given input
        # "Sylvain's approach"
        self.condSigmaMixt = np.zeros((self.numOutputs, self.numOutputs, self.numPts))
        for i in range(self.numPts):
            for j in range(self.numGauss):
                self.condSigmaMixt[:, :, i] = self.condSigmaMixt[:, :, i] + \
                    (self.hi[j, i] ** 2) * self.condSigma[:, :, j]


    def gaussianPDF(self, input, miuInput, covInput):
        dist = multivariate_normal(mean=miuInput.flatten(), cov=covInput)
        return dist.pdf(input)

Results

We encountered multiple hardware issues that were not in the scope of our project along the way. Nevertheless, we managed to solve most of them but at the expense of our original deliverables. Not only did we layed out the pipeline and groundwork for data collection, model training and deployment (on both simulation and the da Vinci robot), but also trained and deployed Gaussian Mixture Models that are able to predict simple trajectories (combinations and variations of straight line + sinusoidal) in real time. For detailed plots and figures, please check out our final report, embedded below.

Conclusion

In this project, not only did I learned a lot about surgical robotics, machine learning, and the mathematics of GMM/GMR, I also gained valuable project management, professional presentation, and technical communication experiences. I was provided with opportunities to improve my core project skillset, including soft skills like professionalism, organization, and teamwork. After the project, I had a better understanding on the concept of maximizing value of a project in a limited time period and built a strong entrepreneurial mindset that would greatly benefit my career in tech.